Tree stack automaton

A tree stack automaton^{[lower-alpha 1]} (plural: tree stack automata) is a formalism considered in automata theory. It is a finite state automaton with the additional ability to manipulate a tree-shaped stack. It is an automaton with storage^[2] whose storage roughly resembles the configurations of a thread automaton. A restricted class of tree stack automata recognises exactly the languages generated by multiple context-free grammars^[3] (or linear context-free rewriting systems).

Definition

Tree stack

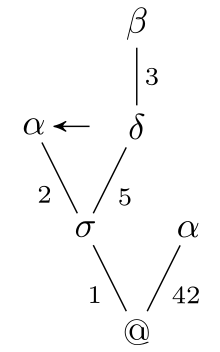
A tree stack with stack pointer 1.2 and domain {ε, 1, 42, 1.2, 1.5, 1.5.3}

For a finite and non-empty set $Γ$ , a tree stack over $Γ$ is a tuple $(t, p)$ where

$t$ is a partial function from strings of positive integers to the set $Γ \cup {@$ } with prefix-closed^{[lower-alpha 2]} domain (called tree),
$@$ (called bottom symbol) is not in $Γ$ and appears exactly at the root of $t$ , and
$p$ is an element of the domain of $t$ (called stack pointer).

The set of all tree stacks over $Γ$ is denoted by $TS(Γ)$ .

The set of predicates on $TS(Γ)$ , denoted by $Pred(Γ)$ , contains the following unary predicates:

$true$ which is true for any tree stack over $Γ$ ,
$bottom$ which is true for tree stacks whose stack pointer points to the bottom symbol, and
$equals(γ)$ which is true for some tree stack $(t, p)$ if $t (p) = γ$ ,

for every $γ \in Γ$ .

The set of instructions on $TS(Γ)$ , denoted by $Instr(Γ)$ , contains the following partial functions:

$id: TS(Γ) \to TS(Γ)$ which is the identity function on $TS(Γ)$ ,
$push n, γ : TS(Γ) \to TS(Γ)$ which adds for a given tree stack $(t, p)$ a pair $(pn \mapsto γ)$ to the tree $t$ and sets the stack pointer to $pn$ (i.e. it pushes $γ$ to the $n$ -th child position) if $pn$ is not yet in the domain of $t$ ,
$up n : TS(Γ) \to TS(Γ)$ which replaces the current stack pointer $p$ by $pn$ (i.e. it moves the stack pointer to the $n$ -th child position) if $pn$ is in the domain of $t$ ,
$down: TS(Γ) \to TS(Γ)$ which removes the last symbol from the stack pointer (i.e. it moves the stack pointer to the parent position), and
$set γ : TS(Γ) \to TS(Γ)$ which replaces the symbol currently under the stack pointer by $γ$ ,

for every positive integer $n$ and every $γ \in Γ$ .

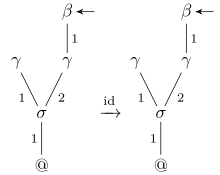Illustration of the instruction id on a tree stack

Illustration of the instruction push on a tree stack

Illustration of the instructions up and down on a tree stack

Illustration of the instruction set on a tree stack

Tree stack automata

A tree stack automaton is a 6-tuple $A = (Q, Γ, Σ, q i, δ, Q f)$ where

$Q$ , $Γ$ , and $Σ$ are finite sets (whose elements are called states, stack symbols, and input symbols, respectively),
$q i \in Q$ (the initial state),
$δ \subseteq fin. Q \times (Σ \cup {ε}) \times Pred(Γ) \times Instr(Γ) \times Q$ (whose elements are called transitions), and
$Q f \subseteq TS(Γ)$ (whose elements are called final states).

A configuration of $A$ is a tuple $(q, c, w)$ where

$q$ is a state (the current state),
$c$ is a tree stack (the current tree stack), and
$w$ is a word over $Σ$ (the remaining word to be read).

A transition $τ = (q 1, u, p, f, q 2)$ is applicable to a configuration $(q, c, w)$ if

$q 1 = q$ ,
$p$ is true on $c$ , and
$f$ is defined for $c$ .

The transition relation of $A$ is the binary relation $⊢$ on configurations of $A$ that is the union of all the relations $⊢ τ$ for a transition $τ = (q 1, u, p, f, q 2)$ where, whenever $τ$ is applicable to $(q, c, w)$ , we have $(q, c, w) ⊢ τ (q 2, f (c), v)$ and $v$ is obtained from $w$ by removing the prefix $u$ .

The language of $A$ is the set of all words $w$ for which there is some state $q \in Q f$ and some tree stack $c$ such that $(q i, c i, w) ⊢ * (q, c, ε)$ where

$⊢ *$ is the reflexive transitive closure of $⊢$ and
$c i = (t i, ε)$ such that $t i$ assigns for $ε$ the symbol $@$ and is undefined otherwise.

Related formalisms

Tree stack automata are equivalent to Turing machines.

A tree stack automaton is called $k$ -restricted for some positive natural number $k$ if, during any run of the automaton, any position of the tree stack is accessed at most $k$ times from below.

1-restricted tree stack automata are equivalent to pushdown automata and therefore also to context-free grammars. $k$ -restricted tree stack automata are equivalent to linear context-free rewriting systems and multiple context-free grammars of fan-out at most $k$ (for every positive integer $k$ ).^[3]

Notes

↑ not to be confused with a device with the same name introduced in 1990 by Wolfgang Golubski and Wolfram-M. Lippe ^[1]
↑ A set of strings is prefix-closed if for every element $w$ in the set, all prefixes of $w$ are also in the set.

References

↑ Golubski, Wolfgang and Lippe, Wolfram-M. (1990). Tree-stack automata. Proceedings of the 15th Symposium on Mathematical Foundations of Computer Science (MFCS 1990). Lecture Notes in Computer Science, Vol. 452, pages 313–321, doi:10.1007/BFb0029624.
↑ Scott, Dana (1967). Some Definitional Suggestions for Automata Theory. Journal of Computer and System Sciences, Vol. 1(2), pages 187–212, doi:10.1016/s0022-0000(67)80014-x.
1 2 Denkinger, Tobias (2016). An automata characterisation for multiple context-free languages. Proceedings of the 20th International Conference on Developments in Language Theory (DLT 2016). Lecture Notes in Computer Science, Vol. 9840, pages 138–150, doi:10.1007/978-3-662-53132-7_12.

Automata theory: formal languages and formal grammars

Chomsky hierarchy	Grammars	Languages	Abstract machines

Type-0 — Type-1 — — — — — Type-2 — — Type-3 — —	Unrestricted (no common name) Context-sensitive Positive range concatenation Indexed — Linear context-free rewriting systems Tree-adjoining Context-free Deterministic context-free Visibly pushdown Regular — Non-recursive	Recursively enumerable Decidable Context-sensitive Positive range concatenation^* Indexed^* — Linear context-free rewriting language Tree-adjoining Context-free Deterministic context-free Visibly pushdown Regular Star-free Finite	Turing machine Decider Linear-bounded PTIME Turing Machine Nested stack Thread automaton restricted Tree stack automaton Embedded pushdown Nondeterministic pushdown Deterministic pushdown Visibly pushdown Finite Counter-free (with aperiodic finite monoid) Acyclic finite

Each category of languages, except those marked by a ^*, is a proper subset of the category directly above it. Any language in each category is generated by a grammar and by an automaton in the category in the same line.

This article is issued from Wikipedia - version of the 10/5/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.